

Given a point P, the pedal triangle of P is the triangle whose polygon vertices are the feet of the perpendiculars from P to the side lines.
1a. We have two situations depends on the place of pedal point :
Here is a graph of Pedal Triangle. In that graph RST is the Pedal Triangle and P is the Pedal point.

Here the pedal point is outside the triangle.
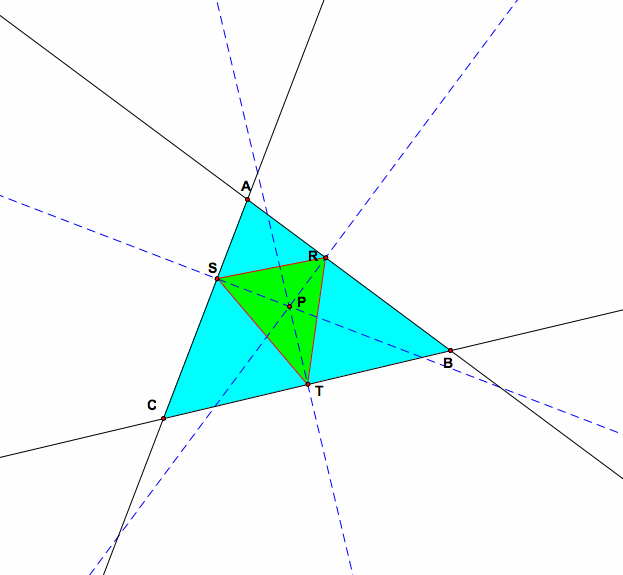
Here the pedal point P is inside the triangle.
1b. Now, how can we graph a pedal triangle? Here is a GSP document which shows a method about how to graph a pedal triangle:
1c. Here P is pedal point of all triangles.
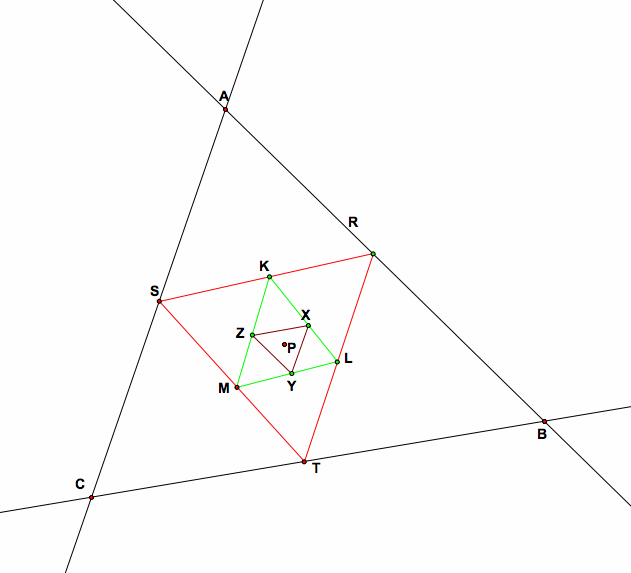
As you see above graph here P is the Pedal point of all triangles which are surrounding one another. In that graph XYZ is the Pedal Triangle of KLM triangle. KLM triangle is the Pedal Triangle of SRT triangle and SRT triangle is the Pedal Triangle of ABC triangle.
A GSP file for how to create this graph: GSP file